Dances with Factors
Dances with Factors
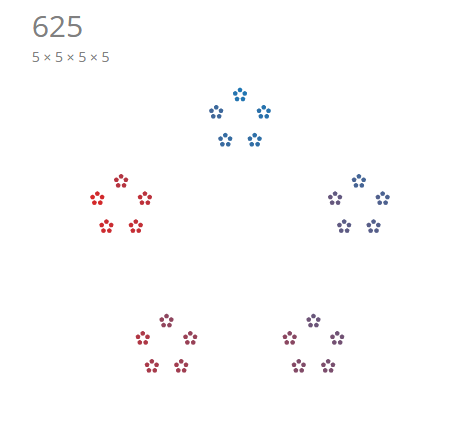
Dances with Factors visualizes prime factorization of integers.
The fundamental theorem of arithmetic states that every integer greater than 1 is either prime itself or a product of prime numbers.
The project is created using D3.js.
Description
Dances with Factors is inspired by the creation of Stephen Von Worley, which in turn is based on the original idea by
Brent Yorgey. Use the control widgets to explore prime factorization of various numbers! You might be interested to check out some
cool numbers e.g. 243, 611, 700, 1024 :)
This visualization helps us track the prime factors that compose a given number. We can easily identify primes when we arrive to a
simple circle (i.e. a prime cannot be composed of smaller divisors). We can also identify common patterns of smaller prime divisors
e.g. 2, 3, 5
An excellent implementation of prime factorization through SVG recursion is provided by Jason Davies. Instead of a recursive
approach, I decided to handle the problem through generating all relevant attributes of points i.e. x, y, and r. This allows me to
provide a data-driven solution to the problem and allow D3 to handle the transitions on new and old points.
Files
index.html: Main HTML file.draw.js: All D3 drawing logic is contained in this file.factor.js: JS file containing logic to compute factors and prime factorization of integers.style.css: stylesheet
Other Notes
Visualizations at larger numbers become less visible due to a fixed viewing dimension and decreasing point radius.
Some interesting visualizations include: